Damn Cool Algorithms: Fountain Codes
Posted by Nick Johnson | Filed under bittorrent, lt-codes, damn-cool-algorithms, fountain-codes
That's right, it's time for another episode of the frustratingly infrequent Damn Cool Algorithms series! If you're not familiar with it, you might want to check out some of the previous posts.
Today's subject is Fountain Codes, otherwise known as "rateless codes". A fountain code is a way to take some data - a file, for example - and transform it into an effectively unlimited number of encoded chunks, such that you can reassemble the original file given any subset of those chunks, as long as you have a little more than the size of the original file. In other words, it lets you create a 'fountain' of encoded data; a receiver can reassemble the file by catching enough 'droplets', regardless of which ones they get and which ones they miss.
What makes this so remarkable is that it allows you to send a file over a lossy connection - such as, say, the internet - in a way that doesn't rely on you knowing the rate of packet loss, and doesn't require the receivers to communicate anything back to you about which packets they missed. You can see how this would be useful in a number of situations, from sending a static file over a broadcast medium, such as on-demand TV, to propagating chunks of a file amongst a large number of peers, like BitTorrent does.
Fundamentally, though, fountain codes are surprisingly simple. There are a number of variants, but for the purposes of this article, we'll examine the simplest, called an LT, or Luby Transform Code. LT codes generate encoded blocks like this:
- Pick a random number, d, between 1 and k, the number of blocks in the file. We'll discuss how best to pick this number later.
- Pick d blocks at random from the file, and combine them together. For our purposes, the xor operation will work fine.
- Transmit the combined block, along with information about which blocks it was constructed from.
That's pretty straightforward, right? A lot depends on how we pick the number of blocks to combine together - called the degree distribution - but we'll cover that in more detail shortly. You can see from the description that some encoded blocks will end up being composed of just a single source block, while most will be composed of several source blocks.
Another thing that might not be immediately obvious is that while we do have to let the receiver know what blocks we combined together to produce the output block, we don't have to transmit that list explicitly. If the transmitter and receivers agree on a pseudo-random number generator, we can seed that PRNG with a randomly chosen seed, and use that to pick the degree and the set of source blocks. Then, we just send the seed along with the encoded block, and our receiver can use the same procedure to reconstruct the list of source blocks we used.
The decoding procedure is a little - but not much - more complicated:
- Reconstruct the list of source blocks that were used to construct this encoded block.
- For each source block from that list, if we have already decoded it, xor that block with the encoded block, and remove it from the list of source blocks.
- If there are at least two source blocks left in the list, add the encoded block to a holding area.
- If there is only one source block remaining in the list, we have successfully decoded another source block! Add it to the decoded file, and iterate through the holding list, repeating the procedure for any encoded blocks that contain it.
Let's work through an example of decoding to make it clearer. Suppose we receive five encoded blocks, each one byte long, along with information about which source blocks each is constructed from. We could represent our data in a graph, like this:
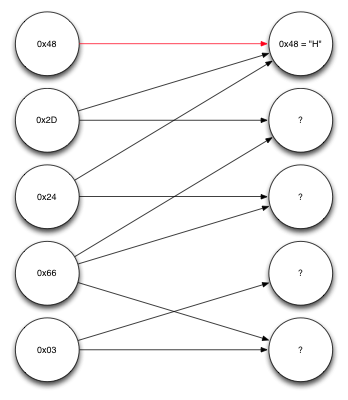
Nodes on the left represent encoded blocks we received, and nodes on the right represent source blocks. The first block we received, 0x48 turns out to consist of only one source block - the first source block - so we already know what that block was. Following the arrows pointing to the first source block back, we can see that the second and third encoded blocks only depend on the first source block and one other, and since we now know the first source block, we can xor them together, giving us this:
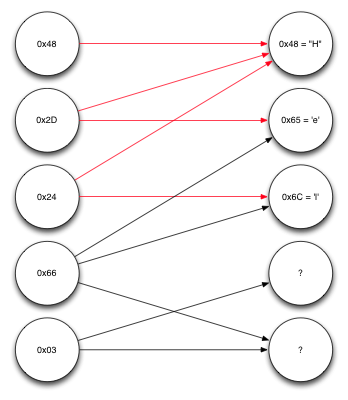
Repeating the same procedure again, we can see we now know enough to decode the fourth encoded block, which depends on the second and third source blocks, both of which we now know. XORing them together lets us decode the fifth and final source block, giving us this:

Finally, we can now decode the last remaining source block, giving us the rest of the message:
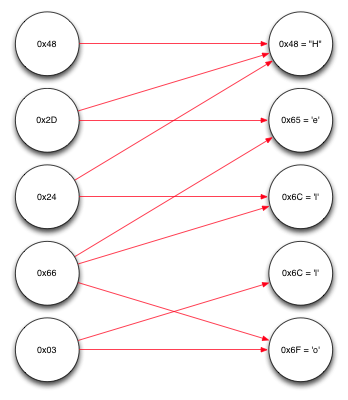
Admittedly this is a fairly contrived example - we happened to receive just the blocks we needed to decode the message, with no extras, and in a very convenient order - but it serves to demonstrate the principle. I'm sure you can see how this applies to larger blocks and larger files quite simply.
I mentioned earlier that the way we choose the number of source blocks each encoded block should consist of - the degree distribution - is quite important, and it is. Ideally, we need to generate a few encoded blocks that have just one source block, so decoding can get started, a majority of encoded blocks that depend on a few others. It turns out such an ideal distribution exists, and is called the ideal soliton distribution.
Unfortunately, the ideal soliton distribution isn't quite so ideal in practice, as random variations make it likely that there will be source blocks that are never included, or that decoding stalls when it runs out of known blocks. A variation on the ideal soliton distribution, called the robust soliton distribution, improves on this, generating more blocks with very few source blocks, and also generating a few blocks that combine all or nearly all of the source blocks, to facilitate decoding the last few source blocks.
That, in a nutshell, is how fountain codes, and LT codes specifically, work. LT codes are the least efficient of the known fountain codes, but also the simplest to explain. If you're interested in learning more, I'd highly recommend reading this technical paper on fountain codes, as well as reading about Raptor Codes, which add only a little complexity over LT codes, but improve their efficiency - both in terms of transmission overhead and computation - significantly.
Before we conclude, though, one further thing to ponder. Fountain codes might look ideal for a system such as bittorrent, allowing seeds to generate and distribute a virtually unlimited number of blocks, more or less eliminating the 'last block' problem for sparsely seeded torrents, and ensuring two randomly chosen peers almost always have useful information to exchange with each other. It suffers from a major issue, though: it becomes very difficult to verify the data you receive from your peers.
Protocols like bittorrent use secure hashing functions such as SHA1, and a trusted party - the original uploader - provides a list of authoritative hashes to all the peers. Each peer can then verify chunks of the file as they're downloaded by hashing them and comparing them to the authoritative hash. With a fountain code, this becomes difficult, however. There's no way to compute the SHA1 hash of an encoded chunk, even knowing the hashes of the individual chunks. We can't trust our peer to compute it for us - they could just lie to us. We could wait until we've got the whole file, and then from the list of invalid chunks, try and deduce what encoded chunks were invalid, but that's difficult and unreliable, and the information likely comes far too late. One alternative would be to have the original uploader publish a public key, and sign every generated block with it. Then, we could verify encoded chunks, but at a cost: now only the original uploader can generate valid encoded blocks, and we lose much of the benefit of using fountain codes in the first place. It seems we're stuck.
There is an alternative, it turns out - a very clever scheme called Homomorphic Hashing, though it has its own caveats and drawbacks - and that's what we'll discuss in the next edition of Damn Cool Algorithms.
Previous Post Next Post